Nama : Evan rafif saputra (11)
Pengertian Pertidaksamaan Irasional
Pertidaksamaan Irasional merupakan suatu bentuk pertidaksamaan yang memuat variabel di dalam tanda akarnya. Bentuk umum pertidaksamaan irasional ialah sebagai berikut ini :

Misal

Langkah – Langkah Penyelesaian
Setelah membaca penjelasan diatas, dibawah ini ada teknik langkah agar dapat menyelesaikan soal pertidaksamaan irasional :
- Pertama menguadratkan kedua ruas pertidaksamaannya supaya bentuk akarnya menjadi hilang, setelah itu menentukan penyelesaiannya.
- Kedua menetapkan syarat bagi fungsi yang berada tepat di bawah tanda akar. Tiap fungsi yang berada di bawah tanda akar tersebut harus menghasilkan nilai yang positif ataupun sama dengan nol (≥ 0).
- Dan yang terakhir menentukan irisan antara penyelesaian utama dengan syarat-syaratnya sehingga dapat diperoleh penyelesaian dari pertidaksamaan irasional tersebut.
Jenis – Jenis Pertidaksamaan Irasional
Berdasarkan langkah – langkah pertidaksamaan irasional diatas, dapat diperoleh bentuk kesimpulan sebagai berikut ini :
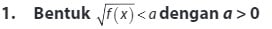
Bentuk ini dapat terpenuhi jika :
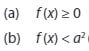
“Tergantung pada tanda pertidaksamaan yang diberikan”.
Penyelesaian : Merupakan irisan dari (a) dan (b)
Contoh :
Tentukanlah himpunan penyelesaian atas pertidaksamaan dibawah ini :
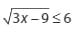
Jawaban :
Bentuk tersebut dapat terpenuhi jika diperoleh :
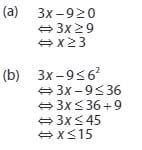
Penyelesaian himpunan pertidaksamaan irasional ini merupakan suatu irisan dari (a) dan (b). Sehingga diperoleh hasil :

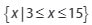
Berdasarkan penjelasan diatas dapat disimpulkan jika hasil himpunan penyelesaian atas pertidaksamaan tersebut ialah disamping ini
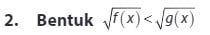
Bentuk ini dapat terpenuhi jika :
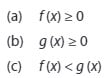
” Sesuai tanda ketidaksamaan yang diberikan”.
Penyelesaian : Merupakan irisan dari (a), (b), dan (c)
Contoh :
Tentukanlah himpunan penyelesaian atas pertidaksamaan dibawah ini :
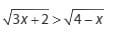
Jawaban :
Bentuk tersebut dapat dipenuhi jika :

Penyelesaian pertidaksamaan irasional adalah suatu irisan dari (a), (b), dan (c). Sehingga diperoleh hasil :
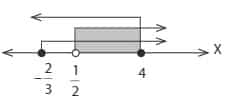
Berdasarkan hasil yang diperoleh diatas dapat disimpulkan hasil dari pertidaksamaan tersebut dibawah ini
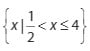
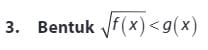
Bentuk ini dapat terpenuhi jika :

Penyelesaian : Merupakan irisan dari (a), (b), dan (c).
Contoh :
Tentukanlah himpunan penyelesaian dari pertidaksamaan dibawah ini
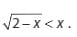
Jawaban :
Bentuk tersebut dapat dipenuhi jika

Titik pembuat nol adalah x = -2, x =1.
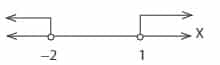
Penyelesaian : x < -2 dan x > 1
Penyelesaian pertidaksamaan irsional merupakan irisan dari (a), (b), dan (c). Sehingga diperoleh :
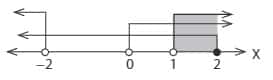
Hasil penyelesaian himpunan pertidaksamaan adalah dibawah ini
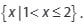
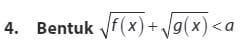
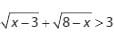
Himpunan penyelesaian dari pertidaksamaan
adalah
A. x > 7
B. 4 < x < 7
C. x < 4
D. -4 < x < 7
E. 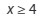
Jawaban :
Bentuk tersebut dapat terpenuhi jika :

Titik pembuat nol x = 4, dan x = 7 adalah sebagai berikut :

Penyelesaian : 4 < x < 7
Penyelesaian himpunan pertidaksamaan irasional merupakan irisan dari (a), (b), dan (c). Sehingga dapat diperoleh sebagai berikut


Tidak ada komentar:
Posting Komentar