Nama : Evan rafif saputra
Kelas : 10 IPS 1
definisi dari pertidakasamaan yaitu suatu fungsi variabel yang diakhiri dengan tanda pertidaksamaan yaitu ( < , >, ≤ , ≥ ). Pertidaksamaan memiliki beberapa jenis yaitu pertidaksamaan bentuk hasil bagi, pertidaksamaan polinomial (suku banyak), pertidaksamaan irasional, pertidaksamaan rasional, pertidaksamaan nilai mutlak, dll. Contoh dari masing-masing pertidaksamaan adalah sebagai berikut:
a. Pertidaksamaan bentuk hasil bagi:

b. Pertidaksamaan polinomial (suku banyak):

c. Pertidaksamaan irasional:
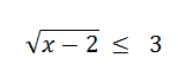
d. Pertidaksamaan nilai mutlak:

Bilangan Rasional

Bilangan rasional adalah suatu bilangan yang bisa diubah dalam bentuk pecahan ab dengan a dan b merupakan bilangan bulat. Ciri-ciri bilangan rasional adalah sebagai berikut:
- Dapat dinyatakan sebagai pecahan biasa. Contoh : 2, -1, ½, ………., dst
- Dapat dinyatakan sebagai pecahan desimal terbatas, seperti : 0,2 ; 0,25; 0,625, ………, dst
- Dapat dinyatakan sebagai pecahan desimal tak terbatas dan berulang, seperti:

- Dapat berupa bilangan yang terletak dibawah tanda akar seperti 1, 4, …..
Bilangan Irasional

Sedangkan bilangan irasional adalah bilangan riil yang tidak bisa dibagi (hasil baginya tidak pernah berhenti). Bilangan irasional tidak bisa dinyatakan sebagai a/b dengan a dan b sebagai bilangan bulat dan b tidak sama dengan nol. Contoh bilangan irasional adalah bilangan π (phi) dan bilangan e (epsilon).
Suatu pertidaksamaan bentuk akar dinamakan juga pertidaksamaan irasional, hal ini dikarekanan nilai peubah yang akan ditentukan selangnya terdapat dalam tanda akar. Teoremanya adalah sebagai berikut:
1.

2.

3.

4.
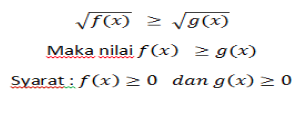
Tips Menyelesaikan Soal

Dalam penyelesaian soal berbentuk pertidaksamaan irasional. Ada beberapa tips dan triknya. Hal ini dikarenakan soal dalam pertidaksamaan irasional mempunyai berbagai tipe. Oleh sebab itu tips dan trik penyelesaian pertidaksamaan irasional adalah sebagai berikut:
1. Mengubah pertidaksamaan irasional ke bentuk umum (ruas kiri berupa bentuk akar)
2. Menentukan nilai ruas kanan
- Jika ruas kanan adalah nol atau positif ( ≥ 0), lakukan langkah-langkah berikut:
- Menentukan penyelesaian akibat kedua ruas dikuadratkan
- Menentukan penyelesaian nilai-nilai yang memenuhi syarat bilangan di bawah tanda akar
- Menentukan irisan ketiga penyelesaian di atas sebagai penyelesaian pertidaksamaan irasional
- Jika ruas kanan bernilai negatif ( < 0), lakukan langkah-langkah berikut:
- Menentukan penyelesaian pertidaksamaan untuk nilai ruas kanan < 0
- Menentukan penyelesaian nilai-nilai yang memenuhi syarat bilangan dibawah tanda akar
- Menentukan irisan kedua penyelesaian di atas sebagai penyelesaian pertidaksamaan irasional
- Jika ruas kanan belum pasti bernilai lebih besar atau sama dengan nol, lakukan langkah-langkah berikut:
- Uraikan nilai ruas kanan menjadi dua kemungkinan yaitu < 0 atau ≥ 0
- Untuk ruas kanan ≥ 0, lakukan langkah-langkah pada bagian a sehingga diperoleh penyelesaiannya
- Untuk ruas kanan < 0, lakukan langkah-langkah pada 2b sehingga diperoleh penyelesaian b.
- Menentukan gabungan penyelesaian a dan b di atas sebagai penyelesaian pertidaksamaan irasional.
Contoh soal: tentukan himpunan penyelesaian dari setiap pertidaksamaan berikut ini:

Jawab:
Tipe soal a adalah bertipe (c ), sehingga cara penyelesaiannya adalah sebagai berikut:
a.

Tipe soal (b) adalah tipe soal yang kedua, oleh sebab itu cara penyelesaiannya adalah sebagai berikut:
b.

definisi dari pertidakasamaan yaitu suatu fungsi variabel yang diakhiri dengan tanda pertidaksamaan yaitu ( < , >, ≤ , ≥ ). Pertidaksamaan memiliki beberapa jenis yaitu pertidaksamaan bentuk hasil bagi, pertidaksamaan polinomial (suku banyak), pertidaksamaan irasional, pertidaksamaan rasional, pertidaksamaan nilai mutlak, dll. Contoh dari masing-masing pertidaksamaan adalah sebagai berikut:
a. Pertidaksamaan bentuk hasil bagi:

b. Pertidaksamaan polinomial (suku banyak):

c. Pertidaksamaan irasional:
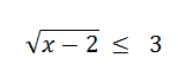
d. Pertidaksamaan nilai mutlak:

Bilangan Rasional

Bilangan rasional adalah suatu bilangan yang bisa diubah dalam bentuk pecahan ab dengan a dan b merupakan bilangan bulat. Ciri-ciri bilangan rasional adalah sebagai berikut:
- Dapat dinyatakan sebagai pecahan biasa. Contoh : 2, -1, ½, ………., dst
- Dapat dinyatakan sebagai pecahan desimal terbatas, seperti : 0,2 ; 0,25; 0,625, ………, dst
- Dapat dinyatakan sebagai pecahan desimal tak terbatas dan berulang, seperti:

- Dapat berupa bilangan yang terletak dibawah tanda akar seperti 1, 4, …..
Bilangan Irasional

Sedangkan bilangan irasional adalah bilangan riil yang tidak bisa dibagi (hasil baginya tidak pernah berhenti). Bilangan irasional tidak bisa dinyatakan sebagai a/b dengan a dan b sebagai bilangan bulat dan b tidak sama dengan nol. Contoh bilangan irasional adalah bilangan π (phi) dan bilangan e (epsilon).
Suatu pertidaksamaan bentuk akar dinamakan juga pertidaksamaan irasional, hal ini dikarekanan nilai peubah yang akan ditentukan selangnya terdapat dalam tanda akar. Teoremanya adalah sebagai berikut:
1.

2.

3.

4.
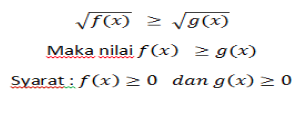
Tips Menyelesaikan Soal

Dalam penyelesaian soal berbentuk pertidaksamaan irasional. Ada beberapa tips dan triknya. Hal ini dikarenakan soal dalam pertidaksamaan irasional mempunyai berbagai tipe. Oleh sebab itu tips dan trik penyelesaian pertidaksamaan irasional adalah sebagai berikut:
1. Mengubah pertidaksamaan irasional ke bentuk umum (ruas kiri berupa bentuk akar)
2. Menentukan nilai ruas kanan
- Jika ruas kanan adalah nol atau positif ( ≥ 0), lakukan langkah-langkah berikut:
- Menentukan penyelesaian akibat kedua ruas dikuadratkan
- Menentukan penyelesaian nilai-nilai yang memenuhi syarat bilangan di bawah tanda akar
- Menentukan irisan ketiga penyelesaian di atas sebagai penyelesaian pertidaksamaan irasional
- Jika ruas kanan bernilai negatif ( < 0), lakukan langkah-langkah berikut:
- Menentukan penyelesaian pertidaksamaan untuk nilai ruas kanan < 0
- Menentukan penyelesaian nilai-nilai yang memenuhi syarat bilangan dibawah tanda akar
- Menentukan irisan kedua penyelesaian di atas sebagai penyelesaian pertidaksamaan irasional
- Jika ruas kanan belum pasti bernilai lebih besar atau sama dengan nol, lakukan langkah-langkah berikut:
- Uraikan nilai ruas kanan menjadi dua kemungkinan yaitu < 0 atau ≥ 0
- Untuk ruas kanan ≥ 0, lakukan langkah-langkah pada bagian a sehingga diperoleh penyelesaiannya
- Untuk ruas kanan < 0, lakukan langkah-langkah pada 2b sehingga diperoleh penyelesaian b.
- Menentukan gabungan penyelesaian a dan b di atas sebagai penyelesaian pertidaksamaan irasional.
Contoh soal: tentukan himpunan penyelesaian dari setiap pertidaksamaan berikut ini:

Jawab:
Tipe soal a adalah bertipe (c ), sehingga cara penyelesaiannya adalah sebagai berikut:
a.

Tipe soal (b) adalah tipe soal yang kedua, oleh sebab itu cara penyelesaiannya adalah sebagai berikut:
b.

Sumber :
https://www.quipper.com/id/blog/mapel/matematika/pertidaksamaan-irasional-dan-rasional-matematika-ipa-kelas-10/


Tidak ada komentar:
Posting Komentar