By Evan Rafif Saputra XI IPS 1
Daftar Isi
I. Pengertian Limit Fungsi Aljabar
II. Sifat-sifat Limit Fungsi
III. Mencari Nilai Limit Fungsi & Contoh Soal
IV. Teorema Limit
V. Limit Tak Tentu
I. Pengertian Limit Fungsi Aljabar
Sebelum mulai memahami konsep dengan lebih mendalam tentang materi limit Matematika dan mencoba menyelesaikan contoh soal limit fungsi aljabar, elo harus memahami pengertiannya dulu.
Nah, limit adalah suatu nilai yang menggunakan pendekatan fungsi saat mendekati nilai tertentu. Kalau bahasa sederhananya, limit dapat dikatakan sebagai nilai yang menuju suatu batas, batas yang bisa dikatakan dekat namun tidak bisa dicapai.
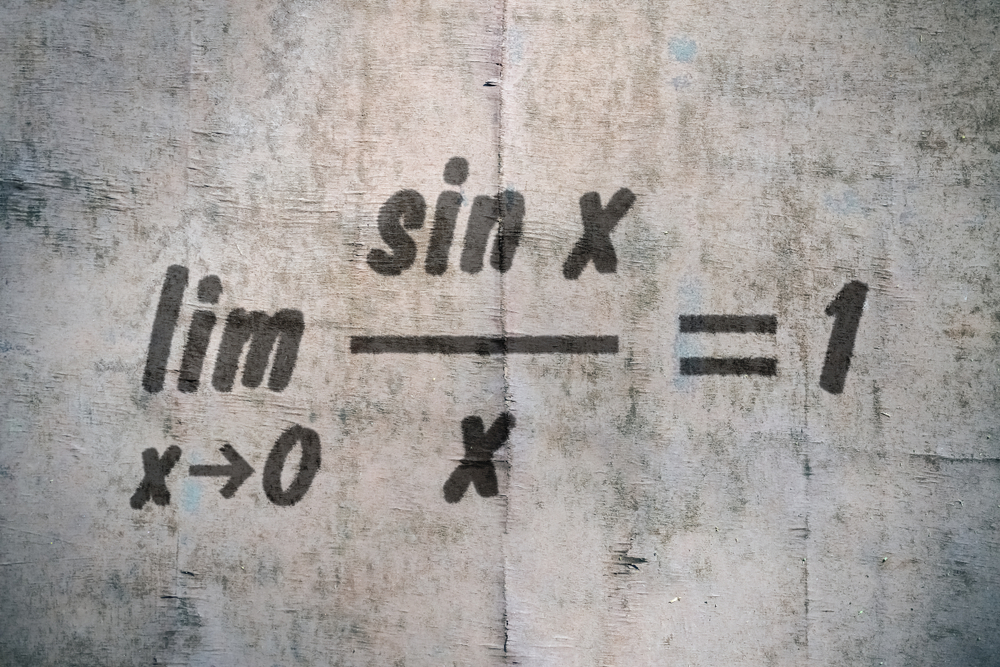
Kok tetep ribet ya? Hehehe… Kalau gitu, coba lihat konsep atau bentuk umum dari limit fungsi di bawah ini:
Limit f(x) mendekati c sama dengan L, ditulis:
jika untuk setiap x yang cukup dekat dengan c tetapi x≠c, f(x) mendekati L.
Gimana? Sudah ada bayangan belum mengenai pengertian limit fungsi aljabar?

II. Sifat-sifat Limit Fungsi
Seperti yang gue jelaskan sebelumnya, sifat-sifat limit fungsi dalam materi limit Matematika fungsi aljabar kelas 11 sangat penting untuk dipahami karena akan berguna sebagai bekal atau dasar saat elo mencari nilai suatu limit dalam soal-soal.
Jadi, untuk memahami dengan benar setiap sifatnya bisa elo lakukan saat mengerjakan latihan soal.
Sifat-sifat limit fungsi aljabar ditentukan jika n adalah bilangan bulat positif, k konstanta, f dan g adalah fungsi-fungsi yang memiliki limit di c, maka selanjutnya berlaku teorema-teorema berikut:
III. Mencari Nilai Limit Fungsi & Contoh Soal
Setelah mengetahui apa saja sifat dari limit, selanjutnya dalam materi limit Matematika, ada cara mencari nilai limit fungsi yang bisa dilakukan menggunakan 3 metode, yaitu metode substitusi, pemfaktoran, dan mengalikan dengan faktor sekawan.
Berikut gue jelaskan dengan lebih lanjut mengenai ketiga metode tersebut lengkap dengan contoh soal limit fungsi aljabar dan pembahasannya.
Metode Substitusi
Metode substitusi merupakan cara yang paling dasar untuk mencari nilai limit. Metode ini dilakukan dengan mensubstitusi langsung nilai kedalam fungsi f(x).
Contoh Soal:
Metode Pemfaktoran
Jika pada metode substitusi menghasilkan suatu nilai bentuk tak tentu seperti:
maka fungsi tersebut harus difaktorkan terlebih dahulu, kemudian baru bisa disubstitusikan.
Contoh Soal:
Metode Mengalikan dengan Faktor Sekawan
Jika pada metode substitusi menghasilkan nilai limit yang irasional, maka fungsi dikalikan dengan akar sekawannya, kemudian bisa disubstitusikan.
Contoh Soal:
1. Soal UNBK SMA IPA 2018 |*Soal Lengkap
Diketahui f(x)={3x−p, x≤22x+1, x>2 Agar limx→2f(x) mempunyai nilai, maka p=...
(A) −2(B) −1(C) 0(D) 1(E) 2
Berdasarkan definisi limit, agar limx→2f(x) mempunyai nilai maka Limit Kiri = Limit Kanan secara simbol dituliskan limx→2+f(x)=limx→2−f(x)=L
Limit kanan limx→2+f(x) limx→2+(2x+1)=2(2)+1=5
Limit kiri limx→2−f(x) limx→2−(3x−p)=3(2)−p=6−p
Berdasarkan definisi agar limx→2f(x) mempunyai nilai yaitu Limit Kiri = Limit Kanan maka: 6−p=5 6−5=p p=1
∴ Pilihan yang sesuai adalah (D) 1
1. Tentukan :
maka nilai limit tersebut adalah…
Jawaban :
2. Tentukan :
maka nilai limit tersebut adalah…
Jawaban :
3. Tentukan :
maka nilai limit tersebut adalah…
Jawaban :
4. Tentukan :
maka nilai limit tersebut adalah…
Jawaban :
5. Tentukan :
maka nilai limit tersebut adalah…
Jawaban :
6. Tentukan nilai
maka nilai limit tersebut adalah…
Jawaban :
7. Tentukan :
maka nilai limit tersebut adalah…
Jawaban :
8. Tentukan :
maka nilai limit tersebut adalah…
Jawaban :
9. Tentukan :
maka nilai limit tersebut adalah…
Jawaban :
10. Tentukan :
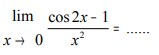
maka nilai limit tersebut adalah…
Jawaban :
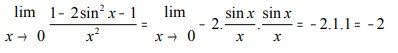
III. Teorema Limit
Limit dalam bahasa umum bermakna batas.
Definisi dari limit ini menyatakan bahwa suatu fungsi f(x) akan mendekati nilai tertentu jika x mendekati nilai tertentu.
Pendekatan ini terbatas antara dua bilangan positif yang sangat kecil yang disebut sebagai epsilon dan delta.
Hubungan ke-2 bilangan positif kecil ini terangkum dalam definisi limit.

Limit 0/0
Bentuk 0/0 kemungkinan timbul dalam
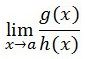
ketika kita menemukan bentuk seperti itu coba untuk sederhanakan fungsi tersebut.
Jika itu bentuk persamaan kuadrat kita bisa coba memfaktorkan atau dengan cara asosiasi, dan jangan lupa aturan a2-b2 = (a+b) (a-b).
Berikut adalah contohnya :

Limit ∞/∞
Bentuk limit ∞/∞ terjadi pada fungsi suku banyak (polinom) seperti :


Rumus cepat limit bentuk ∞/∞

- Jika m<n maka L = 0
- Jika m=n maka L = a/p
- Jika m>n maka L = ∞
IV. Limit Tak Tentu
Fungsi limit tak hingga digunakan untuk menggambarkan keadaan limit x mendekati tak hingga atau dinotasikan dengan lim x → ∞ f(x).
Untuk menyelesaikan limit tak hingga dari suatu fungsi aljabar, terdapat dua cara yang umum digunakan.
Berikut gue jelaskan lebih lanjut mengenai cara-cara tersebut dan juga contoh soal limit fungsi tak hingga dan pembahasannya.
Contoh Soal:
Contoh Soal:
Bentuk (∞-∞) sering sekali muncul pada saat ujian nasional.
Bentuk soalnya sangat beragam. Namun, penyelesaiannya tidak jauh dari penyederhanaan.

Jika disubstitusikan x -> 1 maka bentuknya akan mmenjadi (∞-∞).
Dan untuk menghilangkan bentuk ∞-∞ kita sederhanakan bentuk tersebut menjadi
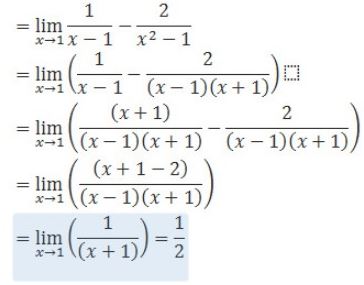
Rumus Cepat limit tak hingga
Rumus cepat mengerjakan limit tak hingga yang pertama dapat digunakan untuk bentuk soal limit tak hingga pada bentuk pecahan.
Untuk memperoleh nilai limit tak hingga bentuk pecahan kita hanya perlu memperhatikan pangkat tertinggi dari masing-masing pembilang dan penyebut.
Ada 3 kemungkinan yang dapat saja terjadi.
- Pertama, pangkat tertinggi pembilang lebih kecil dari pangkat tertinggi penyebut.
- Kedua, pangkat tertinggi pembilang sama dengan pangkat tertinggi penyebut.
- Ketiga, pangkat tertinggi pembilang lebih tinggi dari pangkat tertinggi penyebut.
Rumus ke-3 nilai limit tak terhingga bentuk pecahan tersebut dapat dilihat pada persamaan dibawah ini.
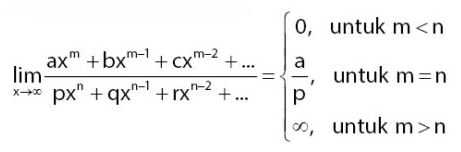

Nilai pangkat tertinggi pada pembilang adalah 3. Nilai pangkat tertinggi penyebut adalah 2 (m>n). Jadi, nilai limitnya adalah ∞.
Sekian Pembahasan Mengenai Materi Limit Kali ini Semoga apa yang tertera di atas dapat membantu menambah pengetahuan kalian yaa!.
Referensi:
https://www.zenius.net/blog/pembahasan-limit-fungsi-beserta-limit-menuju-tak-hingga
https://www.ruangguru.com/blog/konsep-limit-fungsi-aljabar-dan-sifat-sifatnya
https://gurubelajarku.com/limit-fungsi/#Teorema_Limit
https://www.gramedia.com/literasi/limit-fungsi-aljabar/

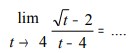
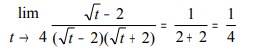
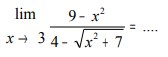
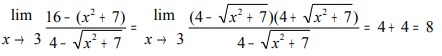
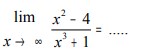
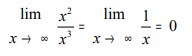
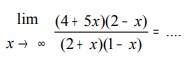
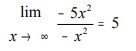
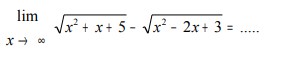
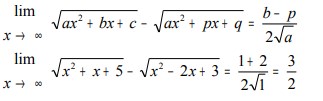


Tidak ada komentar:
Posting Komentar