by Evan Rafif Saputra
Daftar Isi
I. Pengertian Fungsi Al Jabar
II. Rumus Turunan Fungsi Al Jabar
III. Contoh Soal Fungsi Turunan Fungsi Aljabar
IV. Garis Singgung Kurva Dengan Turunan
V. Contoh Soal Garis Singgung Kurva Dengan Turunan
VI. Nilai Stasioner & Turunan Kedua Serta Contoh Soal
I. Pengertian Fungsi Al Jabar
Pertama-tama, kita bahas konsep turunan dulu ya. Dengan memahaminya, kita bisa tahu nih sifat-sifat turunan fungsi aljabar. Coba elo lihat grafik di bawah ini.
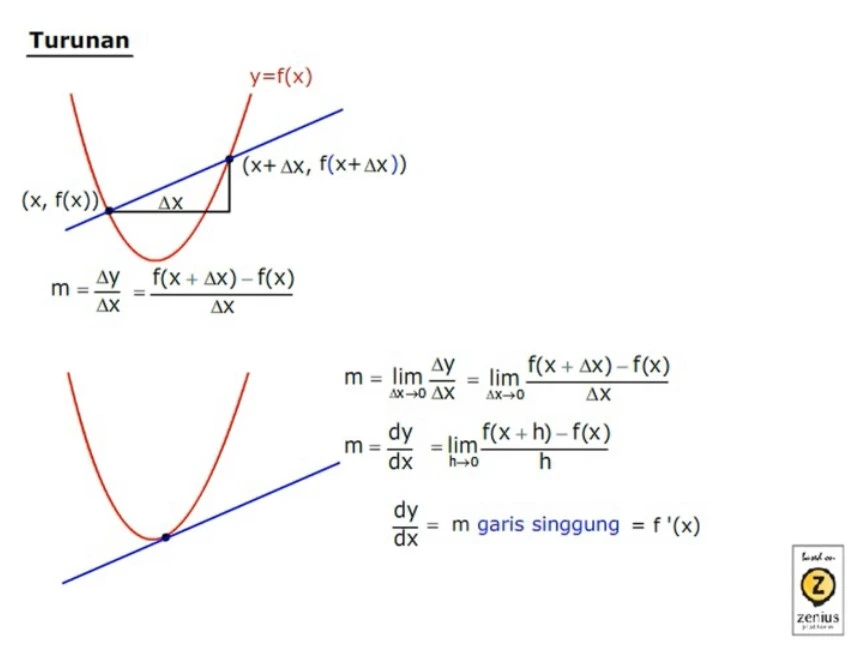
Di grafik di atas, elo bisa melihat ada grafik fungsi y=f(x), yang ditandakan dengan sebuah kurva warna merah.
Selanjutnya, kita coba masukkan dua titik yang membentuk garis biru. Nah, garis tersebut berarti memiliki dua titik, yaitu titik (x, f(x)) dan ((x+Δx), f(c+Δx).
Dari mana Δx itu? Kita bisa lihat, itu dari perubahan jarak dari titik pertama ke titik kedua. Iya, seperti biasa delta (Δ) itu digunakan untuk menggambarkan perubahan nilai ya, Sobat Zenius.
Kembali lagi ke materi, tentunya garis seperti itu memiliki kemiringan alias gradien(m). Elo masih ingat nggak gimana cara nyari gradien?
Ini nih model matematika untuk mencari gradien.
Elo tinggal membagi Δy dengan Δx. Lebih jelasnya, elo bisa baca pada artikel di bawah ini.
Baca Juga: Rumus Gradien (Kemiringan) Garis Lurus dalam Matematika
Nah, kira-kira gimana nih cara dapetin gradien dari grafik di atas? Ya kita tinggal masukkan titik y dan x ke formula tersebut. Bisa kita tuliskan seperti ini.
Selanjutnya, kita andaikan, misalnya dua titik tadi tuh bergeser ke bawah, sampe deket banget, tapi nggak nempel. Berarti ada limit ya, bahwa beda nilainya tuh deket banget sama nol, tapi nggak nol alias nggak nempel.
Nah, dalam keadaan seperti itu, garis lurus tadi menjadi garis singgung seperti di bawah ini.
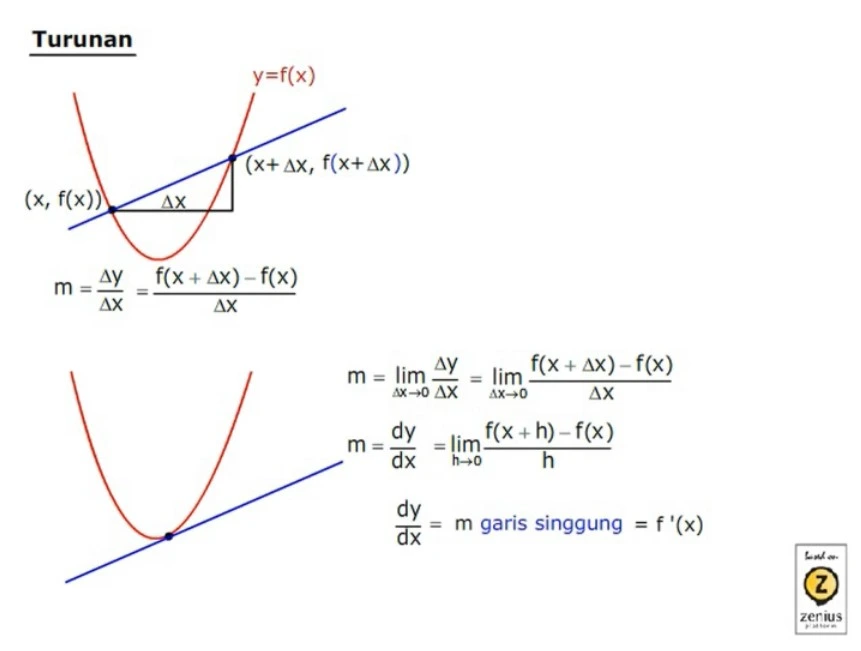
Untuk mencari gradien garis singgung di atas, rumusnya masih sama kan, Sobat Zenius? Cuma, sekarang ada limitnya.
Baca Juga: Memahami Limit Fungsi Aljabar – Materi Matematika Kelas 11
Nah, ini dia nih, gradien garis singgung itu sama dengan definisi turunan yang kita tulis sebagai dy per dx.
Jadi m garis singgung alias dydx adalah turunan f(x), yang dinotasikan sebagai f’(x).
Oleh karena itu, kalo kita simpulkan, gradien garis singgung tadi itu adalah turunan fungsi ya,
II. Rumus Turunan Fungsi Al Jabar
Sesuai dengan pembahasan tentang pengertian turunan tadi, rumusnya itu masih sama ya dengan cara mencari gradien untuk dua titik pada umumnya.
Tapi ingat, ada limitnya. Selain itu, untuk mempermudah pembedaan, Δx pada fungsi turunan biasanya diubah menjadi h. Inilah rumusnya.

Tanda panah kuning di atas menunjukkan bahwa notasi turunan fungsi aljabar itu bisa bermacam-macam ya.
Bisa digambarkan sebagai m dari sebuah garis singgung, bisa juga sebagai dydx, atau sebagai f’(x).
III. Contoh Soal Turunan Fungsi Al Jabar
Untuk contoh turunan fungsi aljabar, kita bahas berbagai macam soal dari yang simpel dulu deh.
Contoh Soal 1: f(x) = 1.000.000
Gimana turunan fungsinya?
Katanya dimulai dari yang gampang, kok langsung dimulai dari 1.000.000? Sebelum elo demo di depan rumah gue, soal ini beneran gampang banget, Sob.
Nih, biar paham dan nggak cuma hafal rumus, kita bikin grafiknya ya.
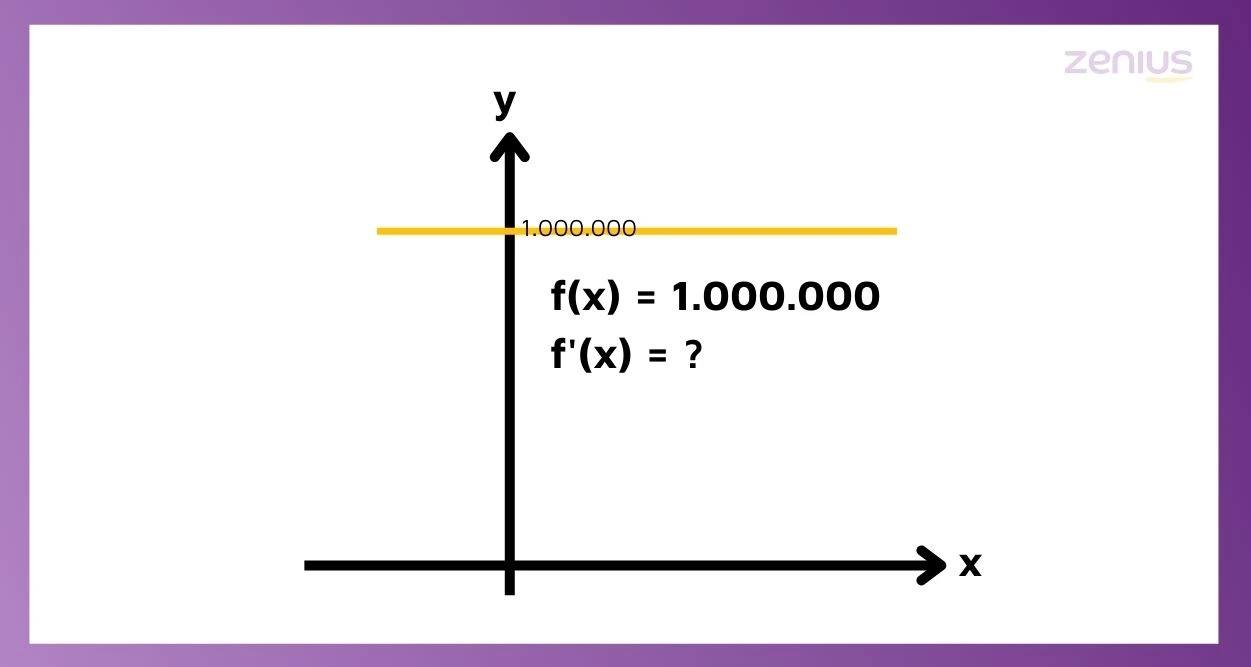
Sobat Zenius, kalo elo beneran paham sama konsep turunan yang udah dibahas tadi, elo sebenarnya bisa tahu jawabannya tanpa pakai rumus apapun lho.
Ingat, turunan fungsi itu kan gradien (kemiringan) garis singgung. Jadi, kalo garisnya lurus kayak gitu, otomatis kemiringannya nol dong.
Sebenarnya, cara gampang lain, kalo di fungsi awal nggak ada x, pasti turunannya nol. Namun, ngerti cara gampang hafalan seperti itu nggak cukup ya. Sebaiknya, kita benar-benar paham konsep serta grafik dari fungsi tersebut.
Nah, biar lebih yakin lagi, gue coba pakai rumus yang tadi deh, buat ngecek apakah benar hasilnya nol.
Wah, beneran ya, hasilnya 0. Dari sini bisa kita simpulkan, berapapun nilainya, mau seratus, sejuta, satu miliar, atau bahkan satu triliun pun, fungsi turunannya akan menjadi nol, bila nggak ada x.
Terus, gimana kalo seandainya ada x? Kita pindah ke soal selanjutnya, yuk.
Contoh Soal 2: f(x)= 2x
Oke, di soal kali ini, ada x nih. Elo familiar nggak sih sama model fungsi seperti itu? Elo harusnya udah pernah ketemu ini ketika belajar fungsi linear.
Simpelnya, kita tinggal input nilai x, untuk mendapatkan nilai f(x) alias y. Kira-kira, grafiknya kayak gimana, nih? Coba gambar dulu ah.
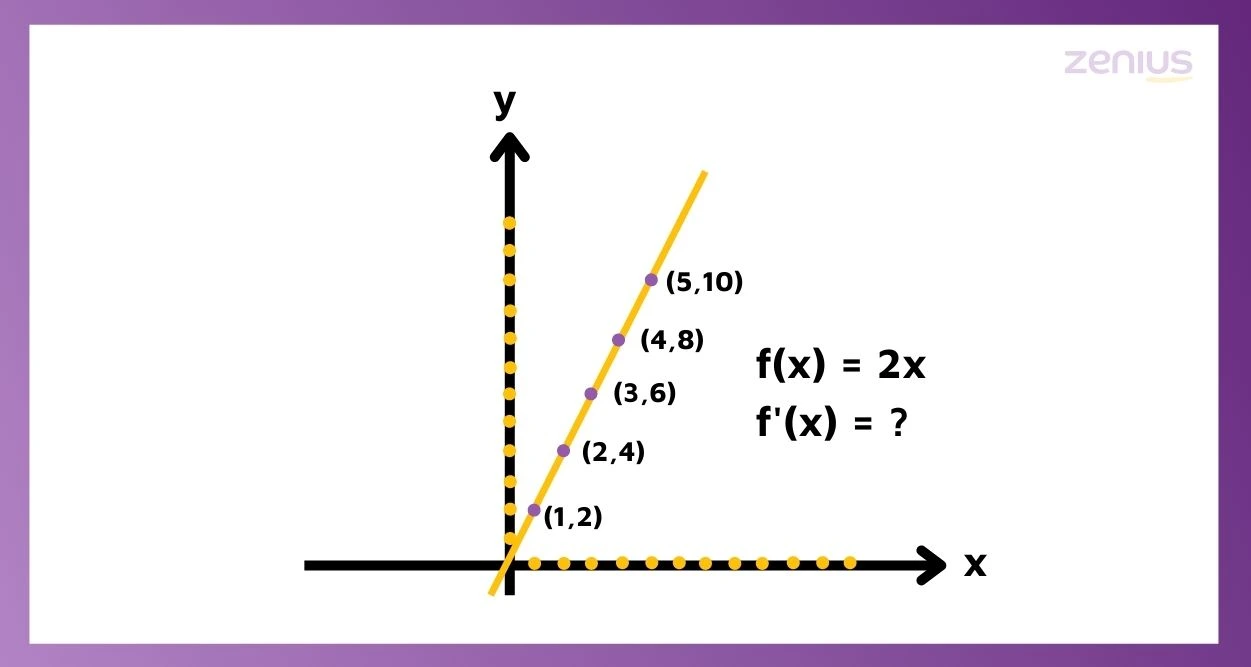
Nah, Sobat Zenius bisa lihat, fungsi tadi membentuk garis lurus dengan gradien nih. Elo masih ingat nggak gimana cara cari gradien garis lurus? Formulanya adalah y=mx+c.
Dari rumus di atas, terlihat bahwa gradien (m) itu menempel dengan x. Berarti berapa nih gradien dari f(x)=2x? Bener banget, gradiennya 2.
Selanjutnya, seperti yang udah kita bahas di bagian pengertian, gradien pada fungsi turunan itu nilainya sama dengan fungsi pertama. Berarti, gradien fungsi turunannya ya 2 juga.
Nih, kita coba tes dengan rumus yang udah kita pelajari ya.
Cara gampangnya, kalo ada angka yang nempel dengan x, pasti angka tersebut adalah gradiennya, Sobat Zenius.
Terus, kalo seandainya ada koefisien, misalnya f(x)=2x+3, gimana nih, Sob? Singkat cerita, tetap 2 jawabannya.
Gampangnya, angka 3 di situ nggak ada x, maka dia jadi nol. Lalu angka yang nempel sama x itu adalah gradien (m), jadi tinggal 2 deh.
Soal No.1
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 15x
b) f(x) = 4
c) f(x) = 12
Pembahasan
⇔f(x) = 15x1
⇔f'(x) = 15x1−1
⇔f'(x) = 15x0
⇔f'(x) = 15
b) f(x) = 4
⇔f(x) = 4x0
⇔f'(x) = 0 ⋅ 4x0−1
⇔f'(x) = 0
c) f(x) = 12
⇔f(x) = 12x0
⇔f'(x) = 0 ⋅ 12x0−1
⇔f'(x) = 0
Soal No.2
Tentukanlah turunan pertama dari fungsi berikut :
a. f(x) = 8x
b. f(x) = x3
c. f(x) = -4x5
d. f(x) = 2x4
e. f(x) = 4x3 - 3x2 + 8x -5
Pembahasan
⇔ f'(x) = 1.8x1-1
⇔ f'(x) = 1.8x0
⇔ f'(x) = 1.1
⇔ f'(x) = 1
b. f(x) = x3
⇔ f'(x) = 3.x3-1
⇔ f'(x) = 3.x2
⇔ f'(x) = 3x2
c. f(x) = -4x5
⇔ f'(x) = -4.5x5-1
⇔ f'(x) = -4.5x4
⇔ f'(x) = -20x4
d. f(x) = 2x4
⇔ f'(x) = 2.4x4-1
⇔ f'(x) = 2.4x3
⇔ f'(x) = 8x3
e. f(x) = 4x3 - 3x2 + 8x -5
⇔ f'(x) = 4.3x3-1 - 3.2x2-1 + 8.1x1-1 - 5.1x1-1
⇔ f'(x) = 4.3x2 - 3.2x1 + 8.1x0 - 5.1x0
⇔ f'(x) = 12x2 - 6x1 + 8x0 - 5x0
⇔ f'(x) = 12x2 - 6x + 8 - 0
⇔ f'(x) = 12x2 - 6x + 8
Soal No.3
Carilah turunan pertama dari fungsi berikut:
f(x) = 4(2x2 + 2x)
Pembahasan
f(x) = 8x2 + 8x
⇔ f'(x) = 8.2x2-1 + 8.1x1-1
⇔ f'(x) = 8.2x1 + 8.1x0
⇔ f'(x) = 16x + 8
Soal No.4
Carilah Turunan Kedua (f"(x)) dari fungsi f(x) = 4x3 - 3x2 + 8x - 5
Pembahasan
f'(x) = 4.3x(3-1) - 3.2x(2-1) + 8 - 0
f'(x) = 12x2 -6x + 8
f"(x) = 12.2x(2-1) - 6 + 0
f"(x) = 24x - 6
Soal No.5
Tentukanlah turunan pertama f'(x) dari fungsi berikut ini:
a. f(x) =
b. f(x) =
Pembahasan
f'(x) = 2.(-1)x(-1-1)
f'(x) = -2x-2
f'(x) = -
b. f(x) =
f'(x) =
f'(x) = -
f'(x) = -
Soal No.6
Tentukanlah turunan pertama dari fungsi berikut ini :
a. f(x) = 3x1/2
b. f(x) = 6x3/2
Pembahasan
⇔ f'(x) =
⇔ f'(x) =
b. f(x) = 6x3/2
⇔ f'(x) =
⇔ f'(x) = 9x1/2
Soal No.7
Carilah turunan f'(x) untuk f(x) = (x2 + 2x + 3)(4x + 5)
Pembahasan
u = (x2 + 2x + 3)
v = (4x + 5)
Sehingga didapatkan
u' = 2x + 2
v' = 4
Kemudian kita masukkan ke dalam rumus f'(x) = u'v + uv' sehingga turunannya menjadi :
f'(x) = (2x + 2)(4x + 5) + (x2 + 2x + 3)(4)
f'(x) = 8x2 + 10x + 8x + 10 + 4x2 + 8x + 12
f'(x) = 8x2 + 4x2 + 10x + 8x + 8x + 10 + 12
f'(x) = 12x2 + 26x + 22
Soal No.8
Diketahui :
f(x) =
Jika f ‘(x) menyatakan turunan pertama f(x), maka f(0) + 2f ‘ (0) =..?
Pembahasan
f(x) =
f(0) =
Sedangkan untuk menentukan turunan terhadap fungsi f(x) yang berbentuk hasil bagi, kita gunakan rumus :
f(x) =
f(x) =
Dengan demikian, kita misalkan :
u = x2 + 3 ⇔ u' = 2x
v = 2x + 1 ⇔ v' = 2
Sehingga turunannya adalah:
f(x) =
f'(x) =
f'(x) =
f'(x) =
Untuk nilai x = 0, maka di dapatkan:
f'(0) =
Sehingga f(0) + 2f'(0) = 3 + 2(−6) = − 9
Soal No.9
Turunan dari fungsi f(x) =
A.
B.
C.
D.
Pembahasan
f(x) =
Dengan demikian :
u = x - 2 ⇔ u' = 1
v = x2 + 3 ⇔ v' = 2x
Sehingga turunannya adalah:
f(x) =
f'(x) =
f'(x) =
f'(x) =
Jawab : D
IV. Garis Singgung Kurva Dengan Turunan
"garis singgung (disebut juga garis tangen) kurva bidang pada titik yang diketahui adalah garis lurus yang "hanya menyentuh" kurva pada titik tersebut." (wikipedia).
Dengan bahasa yang lebih sederhana dapat kita tuliskan garis singgung (tangent line) ialah garis yang hanya memiliki satu titik persekutuan (disebut sebagai titik singgung) dengan kurva.
Dengan pengertian garis singgung di atas, apakah garis pada gambar yang ketiga dibawah ini termasuk garis singgung?
Garis talibusur
atau dapat juga kita sebut dengan garis potong (secant line) yang menghubungkan titik dan pada kurva . Gradien (kemiringan) garis potong adalah:Jika titik
kita geser mendekati titik maka atau semakin kecil yang mengakibatkanjuga semakin kecil.
Dari penjabaran di atas, dengan bahasa yang sederhana dapat kita tuliskan bahwa untuk titik
yang terletak pada kurva , maka gradien garis singgung di titik adalah .V. Contoh Soal Garis Singgung Kurva Dengan Turunan
Contoh Soal 4
Persamaan garis singgung pada kurva y = x6 + 22 yang tegak lurus dengan garis x + 6y = 72 adalah …
Jawab :
x + 6y = 72
6y = — x + 72
y = -1/6 x + 12
m1 = -1/6
Karena tegak lurus maka
m1.m2 = -1
m2 = 6
y = x6 + 22
y’ = m2
6x5 = 6
x5 = 1
x = 1
y = x6 + 22
y = 16 + 22 = 23
y — y1 = m(x — x1)
y — 23 = 6(x -1)
y — 23 = 6x — 6
y = 6x + 17
Contoh Soal 5
Garis singgung kurva y = sin 2x di titik yang berabsis π memotong sumbu y pada koordinat …
Jawab :
x = π
y = sin 2x = sin 2π = 0
m = y’ = 2 cos 2x = 2cos 2π = 2 (-1) = -2
y — y1 = m(x — x1)
y — 0 = -2(x — π)
y = -2x + 2π
titik potong sumbu y → x = 0
y = 0 + π = π
Koordinat titik potong sumbu y adalah (0, π)
Contoh Soal 6
Persamaan garis singgung kurva y = 0,5x2 — 7x + 2 yang membentuk sudut 45o dengan sumbu x positif memotong garis y = 9 — 2x pada koordinat
Jawab :
m = tan 45o = 1
y = 0,5x2 — 7x + 2
y’ = m
x — 7 = 1
x = 8
y = 0,5x2 — 7x + 2
y = 0,5.82 — 7.8 + 2
y = 32 — 56 + 2 = -22
y — y1 = m(x — x1)
y + 22 = 1.(x — 8)
y = x — 30
Selanjutnya kita cari titik potong antara y = 9 — 2x dengan y = x — 30
x — 30 = 9 — 2x
3x = 39
x = 13
y = x — 30 = 13 — 30 = -17
Koordinat titik potongnya (13, -17)
Contoh Soal 7
Garis singgung parabola y = x2 + 10x + 7 di titik yang berabsis 1 menyinggung kurva y = ax3 + b di titik yang berabsis 4. Nilai b = …
Jawab :
x = 1 maka
y = x2 + 10x + 7
y = 12 + 10.1 + 7 = 18
m = y’ = 2x + 10 = 2.1 + 10 = 12
y — y1 = m(x — x1)
y — 18 = 12 (x — 1)
y — 18 = 12x — 12
y = 12x + 6
y = ax3 + b
y’ = m
3ax2 = 12
karena menyinggung di x = 4 maka
3a.42=12
48a = 12
a = 1/4
Kurva menjadi y = 1/4 x3 + b
garis singgung y = 12x + 6
saat x = 4 maka y = 48 + 6 = 54
maka kurva y = 1/4 x3 + b melalui (4, 54)
54 = 1/4 . 43 + b
54 = 16 + b
b = 38
Contoh soal 8
Garis g menyinggung kurva y = x3 — 3x2 + 5x — 10 di titik potongnya dengan garis y=5. Persamaan garis lain yang sejajar g dan menyinggung kurva tersebut adalah ….
Jawab :
Titik potong kuva dengan garis y = 5
x3 — 3x2 + 5x — 10 = 5
x3 — 3x2 + 5x — 15 = 0
x2 (x — 3) + 5(x — 3) = 0
(x2 + 5)(x — 3) = 0
x2 = -5 (tidak mungkin)
x = 3
m = y’ = 3x2 — 6x + 5
m = 3.32 — 6.3 + 5
m = 27 — 18 + 5 = 14
Sekarang kita cari absis titik singgung garis yang lain. Karena sejajar maka gradiennya tetap 14
m = 14
y’ = 14
3x2 — 6x + 5 = 14
3x2 — 6x — 9 = 0
x2 — 2x — 3 = 0
(x — 3)(x + 1) = 0
x = 3 (tidak memenuhi, sebab ini adalah absis titik singgung garis g)
x = -1
y = x3 — 3x2 + 5x — 10
y = (-1)3 — 3(-1)2 + 5(-1) — 10
y = -1 — 3 — 5 — 10 = -19
y — y1 = m(x — x1)
y + 19 = 14 ( x + 1)
y + 19 = 14x + 14
y = 14x — 5
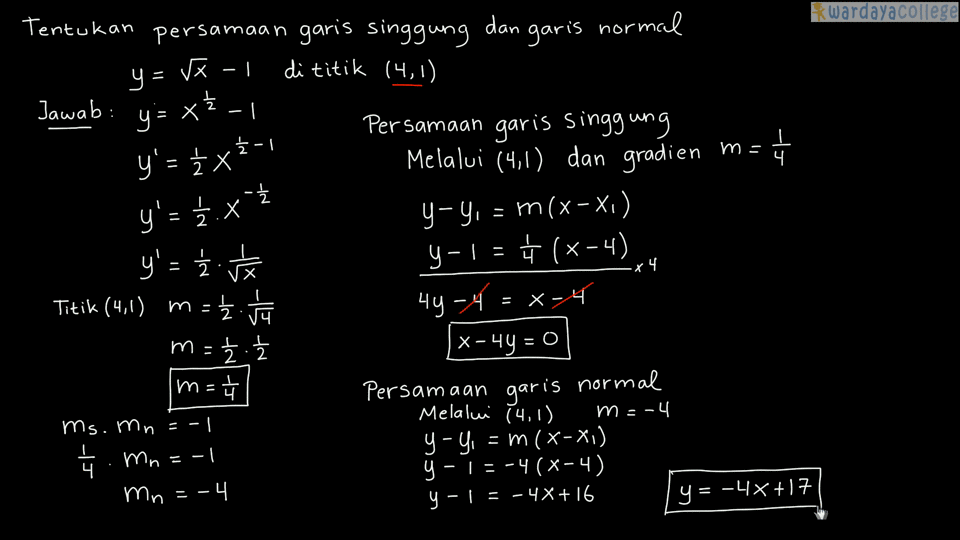
VI. Nilai Stasioner & Turunan Kedua Serta Contoh Soal
Cara Menentukan Nilai Stasioner Beserta Contoh Soal – Dalam ilmu Matematika terdapat pembahasan mengenai titik kritis pada penurunan fungsi atau titik stasioner dalam bidang kalkulus. Pengertian titik stasioner ialah sebuah titik yang memiliki kurva turunan pertama dalam grafik dengan nilai sama dengan nol. Adapula yang mengartikan titik stasioner sebagai titik turun ataupun naik tanda berhenti pada sebuah fungsi.
Titik stasioner pada penurunan beberapa fungsi variabel rill
memiliki turunan parsial sama dengan nol, dimana letaknya di permukaan
grafik. Apakah anda tahu bagaimana cara menentukan stasioner itu?
Bagaimana bentuk contoh soal nilai stasioner itu? Apa saja jenis ekstrim
fungsi itu?
Cara Menentukan Nilai Stasioner Beserta Contoh Soal
Kita tahu bahwa nilai stasioner masih berhubungan dengan turunan fungsi, baik fungsi turun maupun fungsi naik. Cara menentukan stasioner ini dapat dilakukan dengan menyamakan turunannya dengan nol, meskipun nilai turunan pada fungsi turun maupun fungsi naik lebih kecil ataupun lebih besar dari nol (0).
Apabila f(x) diferensiabel dengan f'(a) = 0 di x = a, maka nilai stasioner di x = a ialah f(a) dan titik stasioner dari f(x) ialah titik (a, f(a)). Pada kesempatan kali ini saya akan menjelaskan tentang cara menentukan nilai stasioner beserta contoh soal nilai stasioner. Selain itu saya juga akan membahas tentang jenis ekstrim fungsi lengkap. Untuk lebih jelasnya dapat anda simak di bawah ini.
Seperti yang telah saya jelaskan dalam pengertian titik stasioner di atas bahwa turunan kurva pertama memiliki titik pada grafik yang bernilai sama dengan nol. Dalam hal ini terdapat beberapa persamaan yang menandakan adanya jenis ekstrim fungsi. Untuk itu cara pengerjaan setiap jenis nilai stasionernya memiliki metode yang berbeda beda. Pada umumnya materi nilai stasioner dalam Matematika ini memang perlu dipelajari dan dipahami karena sering muncul dalam soal soal ujian Nasional dan ujian sekolah.
Baca juga : Cara Menghitung Luas Bangun Datar Segi Banyak Beserta Contoh Soal
Latihan Soal Nilai Stasioner
Dalam materi titik stasioner terdapat persamaan f(x) diferensiabel dengan f’(a) = 0 di x = a, maka nilai stasioner di x = a ialah f(a) dan titik stasioner dari f(x) ialah titik (a, f(a)). Cara menentukan nilai stasioner dan cara menyelesaikan contoh soal nilai stasioner tersebut dapat memperhatikan persamaan tersebut. Untuk lebih jelasnya dapat anda perhatikan grafik fungsi di bawah ini:
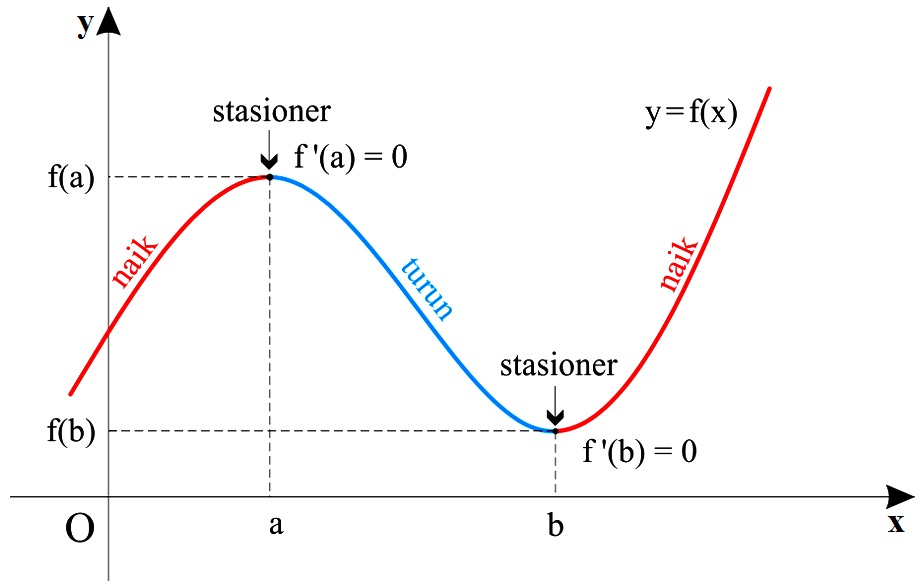
Berdasarkan grafik fungsi di atas dapat kita temukan nilai stasioner di x = a yang berupa f(a) dan nilai stasioner di x = b seperti f(b). Pada titik titik tersebut terdapat nilai turunan pertama yang sama dengan nol. Kemudian untuk titik stasioner pada fungsi f ini dapat berupa titik (a, f(a)) maupun (b, f(b)). Agar anda lebih paham mengenai materi titik stasioner tersebut, maka saya akan membagikan contoh soal terkait materi itu. Berikut contoh soal dan pembahasannya:
1. Diketahui sebuah fungsi x² – 6x. Hitunglah titik stasioner dan nilai stasionernya?
Pembahasan.
Cara menentukan nilai stasioner dari fungsi
tersebut dapat dilakukan dengan mencari turunan pertama dari fungsi
tersebut. Untuk itu hasilnya akan menjadi:
f'(x) = 2x – 6
f(x) stasioner → f'(x) = 0
2x – 6 = 0
2x = 6
x = 3
Untuk mencapai nilai stasioner tersebut dapat dilakukan ketika x = 2. Maka:
Nilai stasioner : f(3) = (3)² – 6(3) = -9
Titik stasioner : (3,-9)
Jadi fungsi tersebut memiliki titik stasioner (3,-9) dan nilai stasioner yaitu -9.
2. Diketahui sebuah fungsi f(x) = x³ – 4x+ 2. Hitunglah titik stasioner dan titik stasionernya?
Pembahasan.
Contoh soal nilai stasioner di atas dapat diselesaikan dengan langkah langkah seperti di bawah ini:
f(x) = x³ – 27x+ 9
f'(x) = 3x² – 27
f(x) stasioner → f'(x) = 0
3x² – 27 = 0
x² – 9 = 0
(x – 3)(x + 3) = 0
x = 3 atau x = -3
Langkah berikutnya yaitu menentukan nilai stasioner dengan nilai x = 3 maupun x = -3. Maka hasilnya akan menjadi:
Nilai stasioner di x = 3 : f(3) = (3)³ – 27(3)+ 9 = -45
Nilai stasioner di x = -3 : f(-3) = (-3)³ – 27(-3)+ 9 = 63
Titik stasionernya ialah (3,-45) dan (-3,63)
Baca juga : Materi Bilangan Bulat (Pengertian, Operasi Hitung dan Contoh)
Penjelasan di atas merupakan cara menentukan nilai stasioner secara umum. Nilai nilai stasioner tersebut dapat dinamakan dengan bakal dari calon nilai ekstrim. Jenis ekstrim fungsi tersebut dapat dibagi menjadi dua kategori yaitu nilai balik minimum dan nilai balik maksimum. Nilai balik minimum dapat dinamakan dengan nilai minimum lokal ataupun nilai minimum relatif. Sedangkan nilai balik maksimum dapat dinamakan dengan nilai maksimum lokal ataupun nilai maksimum relatif. Dalam sebuah fungsi terdapat jenis ekstrim yang dapat dicari menggunakan dua metode yaitu uji turunan pertama maupun uji turunan kedua. Berikut penjelasan selengkapnya:
Uji Turunan Pertama
Cara menentukan jenis ekstrim fungsi yang pertama dapat menggunakan metode uji turunan pertama. Dalam metode ini terdapat beberapa ketentuan seperti di bawah ini:
Apabila nilai stasioner di x = a ialah f(a). Maka:
- f(a) ialah nilai balik maksimum, apabila:
f ‘(x) > 0 (naik), untuk nilai x < a
f ‘(x) < 0 (turun), untuk nilai x > a - f(a) ialah nilai balik minimum, apabila:
f ‘(x) > 0 (naik), untuk nilai x > a
f ‘(x) < 0 (turun), untuk nilai x < a
Agar anda lebih paham mengenai cara menentukan nilai stasioner dalam jenis ekstrim tersebut. Maka saya akan membagikan contoh soal nilai ekstrim terkait ketentuan dalam uji turunan pertama ini. Berikut contoh soal dan pembahasannya:
Diketahui sebuah fungsi f(x) = x³ – 15x² + 12x + 2. Hitunglah jenis ekstrim fungsi tersebut menggunakan uji turunan pertama?
Pembahasan.
Cara menentukan jenis ekstrim dari fungsi tersebut dapat dilakukan dengan mencari turunan pertama dari fungsinya. Maka:
f'(x) = 3x² – 15x + 12
f'(x) = 0
3x² – 15x + 12 = 0
x² – 5x + 4 = 0
(x – 4)(x – 1) = 0
x = 4 atau x = 1
Nilai stasioner pada x = 4 : f(4) = (4)³ – 15(4)² + 12(4) + 2 = -126
Nilai stasioner pada x = 1 : f(1) = (1)³ – 15(1)² + 12(1) + 2 = 0
Uji Turunan Kedua
Selain penjelasan mengenai cara menentukan nilai stasioner di atas. Selanjutnya saya akan membahas tentang cara menentukan jenis ekstrim fungsi menggunakan uji turunan kedua. Dalam uji turunan yang kedua ini terdapat ketentuan seperti di bawah ini:
Baca juga : Contoh Soal Dilatasi Beserta Pengertian dan Rumus Lengkap
Apabila nilai stasioner di x = a ialah f(a). Maka:
- Nilai balik maksimum berupa f(a), apabila f”(a) < 0.
- Nilai balik minimum berupa f(a), apabila f”(a) > 0.
- Belum dapat menetapkan jenis ekstrim, apabila f”(a) = 0 sehingga jenis ekstrimnya dapat ditentukan menggunakan uji turunan pertama seperti di atas.
Agar anda lebih paham mengenai cara menentukan stasioner dalam jenis ekstrim tersebut. Maka saya akan membagikan contoh soal nilai stasioner terkait ketentuan dalam uji turunan kedua ini. Berikut contoh soal dan pembahasannya:
Diketahui sebuah fungsi f(x) = x³ – 15x² + 12x + 2. Hitunglah jenis ekstrim fungsi tersebut menggunakan uji turunan kedua?
Pembahasan.
Cara menentukan jenis ekstrim dari fungsi tersebut
dapat dilakukan dengan mencari turunan pertama dan turunan kedua dari
fungsinya. Maka:
f'(x) = 3x² – 15x + 12
f”(x) = 6x – 15
f'(x) = 0
3x² – 15x + 12 = 0
x² – 5x + 4 = 0
(x – 4)(x – 1) = 0
x = 4 atau x = 1
Nilai stasioner pada x = 4 : f(4) = (4)³ – 15(4)² + 12(4) + 2 = -126
Nilai stasioner pada x = 1 : f(1) = (1)³ – 15(1)² + 12(1) + 2 = 0
Kemudian menentukan uji turunan keduanya menggunakan metode seperti di bawah ini:
f”(4) = 6(4) – 15 = 9 > 0
f”(1) = 6(1) – 15 = -9 < 0
Demikianlah penjelasan mengenai cara menentukan nilai stasioner beserta contoh soal nilai stasioner. Selain itu saya juga telah membahas tentang jenis ekstrim fungsi. Titik stasioner dapat diartikan sebagai titik yang memiliki kurva turunan pertama dalam grafik dengan nilai sama dengan nol. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.
Demikian Pemabahasan kali ini
Terimakasih!!
Referensi :
https://www.zenius.net/blog/turunan-fungsi-aljabar#Pengertian_Turunan_Fungsi_Aljabar
https://www.defantri.com/2020/09/garis-singgung-kurva-dengan-turunan.html
https://www.kontensekolah.com/2020/05/soal-turunan-fungsi-aljabar.html

Tidak ada komentar:
Posting Komentar